Foreword
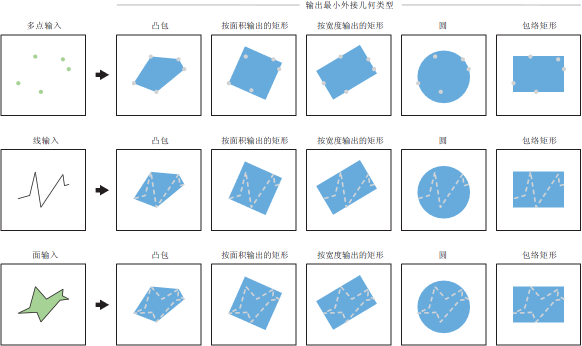
先说问题,给定一个点集,求点集的轮廓,第一眼看过去感觉很简单,直接凸包就能解决了。但是联系到实际的时候凸包太粗糙了,而且情况也太优了,实际想要的要更细节更复杂一些。
这个问题经常出现在ArcGIS地理相关的计算上、图形Mesh等自动创建多边形、又或者是大数据分类划分的时候也可能会用到类似的方法来求轮廓。
凸包
先说简单的解法
Graham Scan算法
-
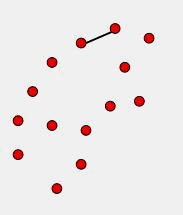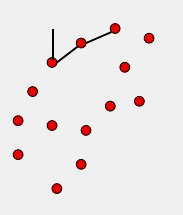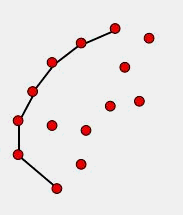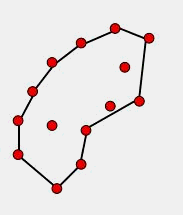
先找到一个Y最低的点作为起始点,
- 然后使用叉积角度判断的方法去判断点的走向,如果走向是凸的那就保留,直到找不到为止。说白了就是求已知点中和当前点所成角度最小的的那个点
- 最终找到第一个点,此时在栈内留下的点序列就是凸包点了。
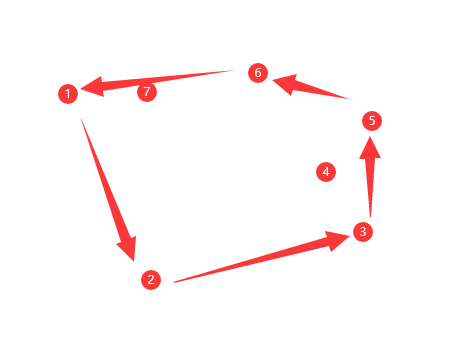
如图所示,最终得到的就是1-2-3-5-6-1 这样一个凸包连线,但是如果我们想要的就是边界办法那要怎么办?
比如下图中的1-2-3-4-5-6-7-1 这样的一个轮廓,两个对比就能看出来凸包有时候圈出来的范围是远大于实际这个点集覆盖的范围的,比如6-7-1 就比6-1所圈的范围要小,如果点集中类似的凹坑比较多或者凹的成都比较大的话,那么求出来的范围偏离实际就比较多。
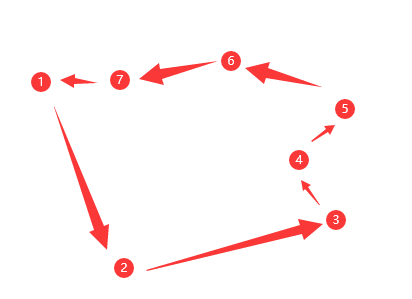
得到的总是类似下面凸包,大范围轮廓
凹包
我们将凸包不能解决的问题归为凹包问题,主要就是希望通过算法能表现出轮廓中的这些凹进去的坑。
滚球法

滚球法算是最简单,最容易理解的,设定一个球有一定的半径,让他沿着点集的边缘运动,只要他不会陷入到其中,那么与他所包含进去的点就是边缘轮廓的点,而相邻两点必然是这个球的弦。
算法:
- 先像凸包那样求出一个Y值最小(Y值相同则取X最大)的点,作为初始点A,此点一定在凹包上。
- 从此点出发,(0,-1)为基准向量,先找一个小于R的边作为初始边,这时这个点即为B,此时一个半径为R/2的圆就卡在了AB上,此时第一个弦AB就找到了。
- 循环寻找接下来的弦,假如上一条弦为DE,则下一条弦必然从E开始,连接到E的一个R领域内的点F。寻找F可以使用如下的原则:先对E的R领域的点,以E为中心EO向量为基准进行极坐标方向排序,之后依次为R领域点F0~FN建立以EFi为弦的圆,然后检查其中是否包含其他F0~FN的点,若不存在,则EFi即为新弦,则跳出循环。
- 依次找到所有的弦,直到找不到新弦或遇到以前已经作为弦的点为止。
如果这个R选择足够合适,那么大概率可以得到一个凹的轮廓。
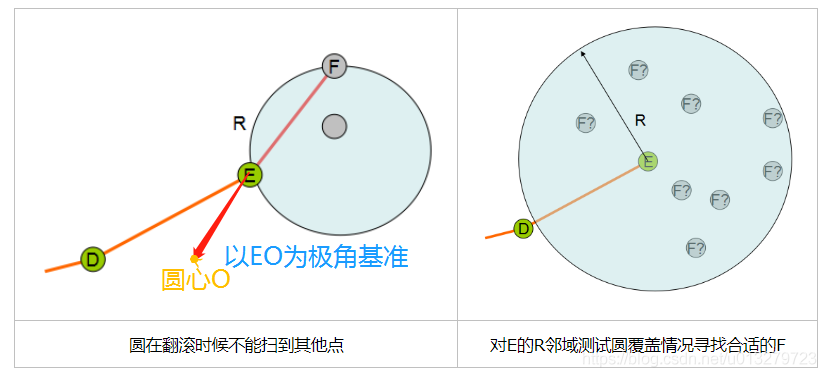
为什么这里说的是大概率,因为有可能你的点集不够集中,那么这个时候R就会出现要么过大要么过小,没有一个合适的值。
R的寻找
有些时候我们只需要一个轮廓,而不是将点汇聚成多个轮廓。那么这个时候这个R要怎么确定。简单说这个最合适的R应该是:任意一个点距离他最近3个点的最大距离(这3个点应该是不共线的,否则会遇到下面的缺陷中提到的问题),这样就不会有点被孤立起来了。
缺陷
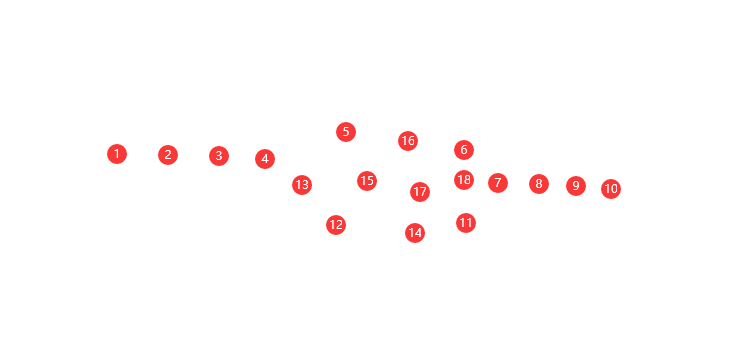
滚球法有个问题,如果出现单边直线,比如下图中的1-2-3-4和 7-8-9-10 这两条都是完全平行的直线,那么滚球法这里无法正确滚到这几个点。需要通过R来排除这种共线的情况
建议
滚球法需要多次寻找在圆内的点或者是点附近的点(圆半径)这种,所以最好这里直接使用KD树来存储点,这样后面计算的时候,计算量会小很多,只是存储构建的时候稍微慢了一点而已。
Delaunay三角化
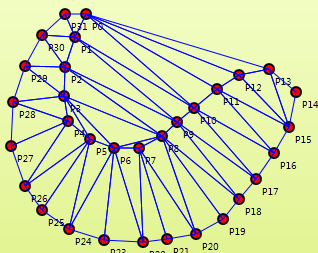
Delaunay三角化可以让点集形成如图所示的三角网络,如果不删边,这个时候这个图就是一个凸包。通过选择性删边,可以得到一个凹包的效果。
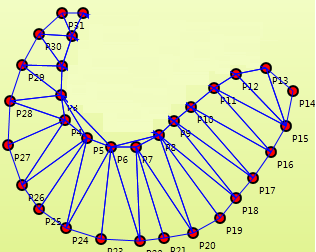
- 为点集S求取Delaunay三角网M,三角网用标准Mesh形式表示。
- 为M初始化所有Edge对象,并求取Edge的长度以及邻接三角形集合。其中邻接2个三角形的边为内部边,只有1个三角形的为边界边,0个三角形的边作为计算过程中会退化的边。
- 将所有长度大于R的边界边加入队列,并当队列非空时循环下列过程:
- 从队列中取出一条边E,得到E的唯一邻接三角形T1。
- 找到T1的另外两个边E1,E2,从他们的邻接三角形集合中删去T1。
- 将E1,E2中新形成的长度大于R的边界边加入队列。
- 将E置无效标记,若E1,E2有退化的,也置无效标记。
- 收集所有有效的边界边,形成边列表,输出。
这种通过三角Mesh的方式来计算凹报,其实也需要一个参数R,作为删边的标准。
Summary
通过以上的算法,都可以得到一定程度上的边界,但是实际应用的时候会发现这还不够。不够的地方,主要是对边界的描述,有时候你认为这里该凸还是该凹,这都是基于你当前的认知或者是R,但是只用一个R显然是不足以描述我们的问题的,所以我考虑的是将这个R与点所在位置的点集密度联系起来,从而让这个R是一个动态R,这样可以让这个凹包显得更凹一些,保留的细节也会更多一些。
Quote
https://blog.csdn.net/u013279723/article/details/108085334
https://www.cnblogs.com/liweis/p/4749096.html
https://www.cnblogs.com/chnhideyoshi/p/ConcaveHull.html?utm_source=tuicool&utm_medium=referral