Foreword
RVO已经实际应用了,但是基于RVO的论理,还是做了进一步修改,将RVO和实际应用结合的更紧密一些。
或者说实际上模拟了一个小型物理系统,来追踪和获取路径点信息。
本文会长期更新,直到所有未明问题得到解。
先说一下实际应用的坑
1.RVO2 3D 这里官方给的例子是VS,直接可以上手运行,而git上的例子不是基于vs的,不是很好编译
https://gamma.cs.unc.edu/RVO2/
https://github.com/snape/RVO2
2.RVO2 3D缺少了一些关键参数,比如加速度,实际控制中没有加速度控制,可能和实际应用多有不同,而2D版本则是都有的。有尝试过使用别人增加加速度控制的,但是实际上效果不好,可能需要重新实现一下。
3.RVO2 3D中速度的限制或者物理量的单位不明确,特别是速度和TimeStep,当时间精度和速度都设置为真实物理量的时候,会发现速度往往是设置值的10倍,而有时候又是正常的,这个可能是实现的内部有bug,导致这个物理量成了一个相对值,而不是绝对值,不能真的当作物理量对待。这就导致获取到了RVO的路径点以后,还需要将这一段路径点重新转化成你的物理环境下的变量,而不能直接拿来用。
4.TimeHorizon,这个东西会严重影响智能体是否能达到最高速度,严重影响最终能否获取到结果,但是实际意义又不明确,导致用起来很难。
5.RVO2 3D 中没有实现障碍物的处理,2D中则是给了一些障碍物模型。需要添加障碍物,要重写。
6.RVO中的算法是相同的,智能体之间不需要交流,这个不能算缺点,不需要交流的好处是,他们可以应用到分布式中,只要他们能拿到相同的信息即可得到相同的结果,从而可以在分布式的环境下独立运行,而不出现干扰。同理这样的情况下会导致可能某些情况下效率不高,需要更高一层的算法帮忙做好局部目标来缓解局部低效的情况(比如很窄的通道,两边都挤满人的情况下,RVO这个时候局部避障可能大概率走不出来)
优点
- 简单,计算量不大。
- 实时可控,解算速率比较快,中途可以加入新节点也可以移除老节点。
- 开源,可以根据基础算法二次扩展,适配实际的应用环境。
- 解耦路径规划,本身只处理局部碰撞即可,全局的路径对他来说并不知道。
框架
-
全局寻路算法,给出中间的路径点(roadmap或者a*之类的)
- 路径点作为输入,给到RVO,作为局部目标点,到达局部目标点后,继续朝下一个局部目标点行进,直到最终目标点
- 转换并且平滑RVO路径点,将其合理化到对应的物理世界中
- 输出路径点,开始执行
RVO理论基础
要说RVO需要先理解VO的理论基础
VO
- Velocity Obstacles
VO简单理解,只要两个点本身在未碰撞的情况下,将其中一个点化作质点,其每次速度更新,都选择不会与另一点相交的速度方向,那么二者即不会碰撞。
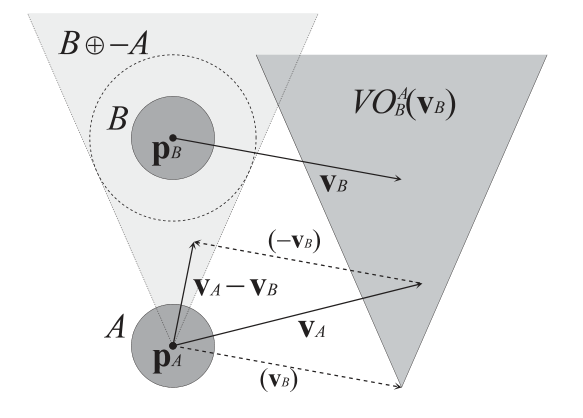
比如上图中,将A当作一个质点,B是有半径的物体。A相对于B的速度就是$V_A - V_B$ ,那么他们的碰撞区域就是上图中的浅色三角区域,即
\[B\bigoplus -A\]但是由于实际计算的时候求得不是相对速度,而是实际的$V_A$的速度,所以会再加上$V_B$,那么这个浅色三角形就会整体偏移,变成深色三角形。
并将这个深色三角形定义为
\[VO_B^A( { V_B })\]这里所有速度都单纯的指二维平面,矢量速度
-
A,B是一个智能体
-
$P_A$ 是A的当前位置, $P_B$ 是B的当前位置
-
$ VO_B^A( { V_B })$ 是指当B以 $V_B$ 的速度运动时,会与A发生碰撞的,所有A的速度的集合
-
$ \lambda (p,v) = \lbrace p+tv \mid t >=0 \rbrace $ 是一个以p为原点,v为方向的射线,t为时间,总体就是质点p可以运动的一个范围
所以总的公式就是
\[VO_B^A(V_B)=\lbrace V_A| \lambda (p_A,V_A-V_B) \bigcap B \bigoplus -A \neq 0 \rbrace\]这样定义出来的就是AB碰撞的速度区域集合,而只要速度不属于这个区间,那么就可以保证不会碰撞。
这里统一都是使用速度方向,而没有速度大小的概念
其他解释
- Minkowski sum,闵可夫斯基和,官方定义:两个图形A,B的闵可夫斯基和 $C=\lbrace a+b|a∈A,b∈B \rbrace C=\lbrace a+b|a∈A,b∈B \rbrace$ 通俗一点:从原点向图形A内部的每一个点做向量,将图形B沿这个向量移动,所有移动后的B所形成的图形便是闵可夫斯基和(具有交换律),一般都是指凸包
- 部分数学基础,https://www.cnblogs.com/xzyxzy/p/10033130.html
RVO
- Reciprocal Velocity Obstacles
RVO主要是解决VO中速度抖动的问题,同时他基于VO给出了几条推论
第一个是如果$v_A ∈VO_B^A( { V_B })$ 那么对应可以推出来 $V_B ∈VO_A^B( { v_A })$ ,简单说碰撞是2个人的事情,你碰了我,那么我必然也碰了你,力的作用是相互的,也就是对称性
第二个是基于上一条,在碰撞的基础上,如果二者的速度同时增加或者减少某一个量,依然会碰撞,这个应该叫同步性
第三个是在$ VO_B^A( { V_B })$的左侧或者右侧的任意2个速度,他们加减后同理也在$ VO_B^A( { V_B })$ 的左侧或者右侧,加减的程度不超过他们本身的速度。
\[v_A \notin VO_B^A( { V_B })\land v_A' \notin VO_B^A( { V_B }) \Rightarrow ((1-\alpha)v_A + \alpha v_A') \notin VO_B^A( { V_B }) | 0<=\alpha <=1\]感觉上面就是简单的交换律和结合律就能验证的东西。
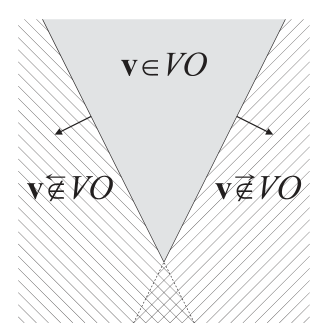
接着就是验证VO会发生速度抖动的情况:
- 假设初始状态为会发生碰撞:$v_A ∈VO_B^A( { V_B }) V_B ∈VO_A^B( { v_A })$
- 由于在对方的VO内,所以各自选择新的速度以防止碰撞:$v_A’ \notin VO_B^A( { V_B }), v_B’ \notin VO_A^B( { V_A })$
- 由前面VO的Symmetry性质可知:此时,原来的速度不在当前速度的VO内:$v_A \notin VO_B^A( { V_B’ }), v_B \notin VO_A^B( { V_A’ })$
- 而由于VA的设定,更倾向于目标速度,也就是老速度$V_A,V_B$,则又会回到原来的$V_A,V_B$
- 于是在1→4之间循环,即发生抖动
RVO则是在这个基础上(VO将对方当作静态障碍物,认为对方不能移动,向对来说比较保守),改变了速度选择的策略,认为每个智能体会为对方考虑,即各承担一半的责任,这就是Reciprocal的含义。
\[RVO_B^A(V_B,V_A)=\lbrace V_A'| 2V_A'-V_A \in VO_B^A(V_B) \rbrace\]这里的$V_A’$其实就是$(V_A+V_B)/2$
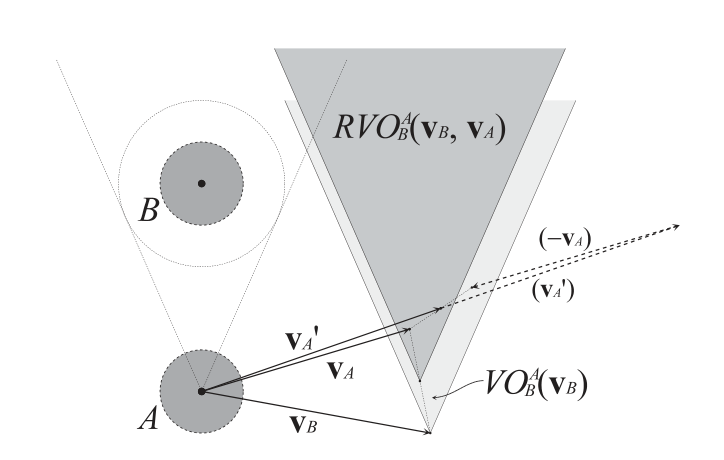
为什么这样,就没有抖动了,是因为选择后的$V_A’$在一下轮循环中依然是最接近目标速度的速度,而不会出现又切回到老速度的情况。
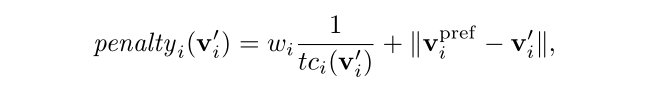
在过度拥挤的情况下,无法找到一个合适速度的时候,就会选择一个碰撞内的速度,按照惩罚函数,求得一个轻惩罚的速度。
其中w是一个描述智能体是激进一些还是保守一些的参数,越激进相当于会做出更危险一点的行动,更轻视碰撞时间的影响。
同时为了简化计算,RVO设置了邻近计算距离,最佳距离是通过碰撞时间,距离,模拟精度以及平均速度等计算得来的
RVO2/ORCA
- Optimal Reciprocal Collision Avoidance
简单说就是基于RVO理论的调优,将计算复杂度降低成低维度的线性规划问题。可以把论文作为RVO算法的一次理论实践,对实现细节给出了具体说明和调优等。
由于这里是具体的实践,所以又增加了一部分定义
- rA,A的半径,可以认为A是个球,这是他的安全半径
- VA_pref,A的目标速度或者期望速度矢量
- VA_max,A的最大速度
结合之前的PA和VA,这些量被认为是一个智能体的内部具有的状态。
之前的RVO和VO都是只基于速度方向考虑,不考虑速度的具体大小,但是实际上每个智能体的速度是有限的,多数情况下只能小不能大,ORCA于是基于此添加了部分定义,考虑的细节更接近实际了。
首先是引入了类时间定义,即可以知道速度大小或者说路程大小了,同时碰撞也变成了两个球体碰撞,而不是之前的质点和球体碰撞,如图a所示。图b中显示了,当质点A达到红线时会发生碰撞,而此时速度值为绿色弧线上对应的点。
- $D(p,r)$ ,表示以p为圆心,r为半径的圆
- $VO^\tau_{A \vert B} = \lbrace v \vert\exists t \in [0,\tau],tv \in D(p_B - p_A,r_A+r_B) \rbrace $ 表示的就是绿弧以及左右两条边组成的图形,这个区域的速度就是会碰撞的速度
- $CA_{A\vert B}^\tau(V_B) = \lbrace v\vert v \notin VO_{A\vert B}^\tau \bigoplus V_B \rbrace$ ORCA就是要从这里选择一个最优的速度,并且其不是在碰撞区域内的
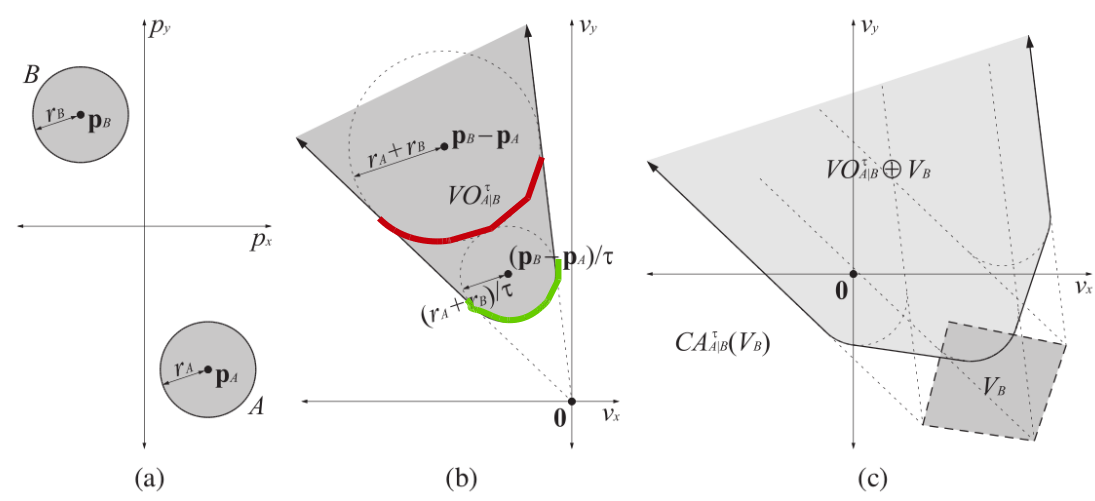
最优的速度是怎么选呢:
$V_A^{opt}$ 和 $V_B^{opt}$ 首先都满足$CA_{A\vert B}^\tau(V_B)$ , 同时最好他们又能满足$D(v^{opt},r^{opt})$ ,其中$v^{opt}$ 是最接近目标方向的速度,即V_pref ,$^{opt}$则是这个速度的允许的接近范围。最好的情况下A和B都能在范围内找到合适的并且接近目标速度的速度。
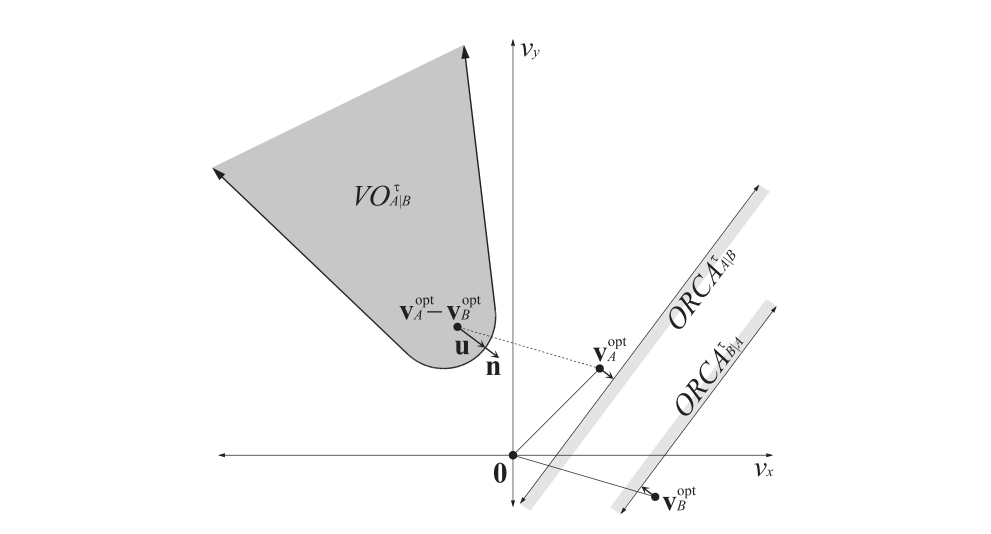
其中n是u的同向法向量,v·n>=0表示一个平面,u是最小偏移
\[u = (^{argmin}_{v \in \partial VO_{A|B}^\tau }||v-(v_A^{opt}-v_B^{opt})||)-(v_A^{opt}-v_B^{opt})\]但是也有一些情况会无解,比如被包围,这种情况下无法选出来一个合适的速度
\[v_A^{new} = ^{argmin}_{v \in D(0,v_A^{max})} {_{B \neq A}^{{max} \space d_{A|B}(V)}}\]-
$d_{A \vert B}(V)$ 表示速度的越界程度,正表示在ORCA外,负表示在ORCA内,值为距离
\(_{B \neq A}^{{max} \space d_{A|B}(V)}\) 求最大的越界程度,也就是最小违规值
所以合起来就是取违规程度最小的可行速度。
他的整体思路就是这样:
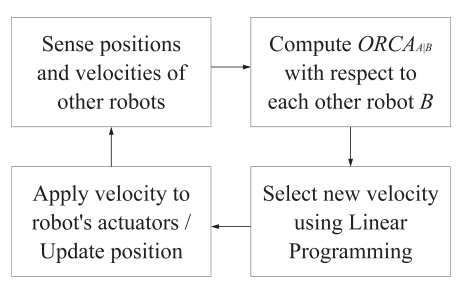
- 获取到位置和速度信息
- 计算每个附近的智能体的 $ORCA_{AB}$ ,然后选择一个最接近的速度
- 将速度给到当前智能体,更新其位置
- 循环1-3,直到到达目标位置
AVO2
- Reciprocal Collision Avoidance with Acceleration-Velocity Obstacles
VO是通过选择速度来避障,AO则是通过选择加速度来避障,但是单纯的选择加速度没法保证不碰撞。而AVO就是结合加速度对速度进行约束,从而让最后给出的路径更加平滑,符合实际。
代码详解
先说代码和实际论文有挺大区别得,有很多东西都没有详细解释,而且是做过一定程度上计算优化的,所以好多都是直接得到结果,所以有些地方看不懂。
整体结构比较简单,每个对象都叫做agent,然后他们有对应的属性,首先给他们初始化然后将其加入到模拟器中即可。
接着就是整体大循环,每次可以更新每个agent的目标位置,然后更加rvo理论,更新agent的属性,最终到达目的地。
这部分代码是基于RVO2D的版本
RVOSimulator更新逻辑
RVOSimulator也很简单,首先是创建KDtree,然后每个agent更新自己的邻近点,并且更新自己的速度。
然后就是所有agent根据新速度更新位置,关键主要是在更新速度中
void RVOSimulator::doStep()
{
kdTree_->buildAgentTree();
#ifdef _OPENMP
#pragma omp parallel for
#endif
for (int i = 0; i < static_cast<int>(agents_.size()); ++i) {
agents_[i]->computeNeighbors();
agents_[i]->computeNewVelocity();
}
#ifdef _OPENMP
#pragma omp parallel for
#endif
for (int i = 0; i < static_cast<int>(agents_.size()); ++i) {
agents_[i]->update();
}
globalTime_ += timeStep_;
}
computeNewVelocity
agent速度计算逻辑,这部分逻辑比较复杂,比较多,我们先看整体
整体上是先计算邻近的所有静态的障碍物,得到障碍物的边,或者说障碍线。
然后就是统一计算邻近的每个agent的障碍线,最后将这些障碍线和agent的一些属性带进去求线性规划的解
/* Search for the best new velocity. */
void Agent::computeNewVelocity()
{
// 这是一个线的集合
orcaLines_.clear();
// 将timehorizon倒数
const float invTimeHorizonObst = 1.0f / timeHorizonObst_;
// 这里主要是处理静态的障碍物
/* Create obstacle ORCA lines. */
for (size_t i = 0; i < obstacleNeighbors_.size(); ++i)
const size_t numObstLines = orcaLines_.size();
// 将timehorizon倒数
const float invTimeHorizon = 1.0f / timeHorizon_;
/* Create agent ORCA lines. */
for (size_t i = 0; i < agentNeighbors_.size(); ++i)
size_t lineFail = linearProgram2(orcaLines_, maxSpeed_, prefVelocity_, false, newVelocity_);
if (lineFail < orcaLines_.size()) {
linearProgram3(orcaLines_, numObstLines, lineFail, maxSpeed_, newVelocity_);
}
}
障碍物
这个障碍物的处理,实话实说没看懂,原论文中根本没说这个。根据我看的我猜测大概意思是障碍物由于是静态的,所以比较容易计算出来对应的RVO的区域。由于那个障碍物可能存在大的遮挡小的之类的问题,为了得到准确的范围,所以下面写的非常复杂?
// 这是一个线的集合
orcaLines_.clear();
// 将timehorizon倒数
const float invTimeHorizonObst = 1.0f / timeHorizonObst_;
// 这里主要是处理静态的障碍物
/* Create obstacle ORCA lines. */
for (size_t i = 0; i < obstacleNeighbors_.size(); ++i) {
//拿到邻近的障碍物
const Obstacle *obstacle1 = obstacleNeighbors_[i].second;
// 拿到障碍物旁的障碍物?
const Obstacle *obstacle2 = obstacle1->nextObstacle_;
// 获取2个障碍物的相对位置
const Vector2 relativePosition1 = obstacle1->point_ - position_;
const Vector2 relativePosition2 = obstacle2->point_ - position_;
/*
* Check if velocity obstacle of obstacle is already taken care of by
* previously constructed obstacle ORCA lines.
*/
bool alreadyCovered = false;
// 大概就是有可能有一个大障碍物,挡在一个小障碍物前面,而大障碍物已经处理过了,这个时候小障碍物再处理的时候,就会发现没必要了?
for (size_t j = 0; j < orcaLines_.size(); ++j) {
if (det(invTimeHorizonObst * relativePosition1 - orcaLines_[j].point, orcaLines_[j].direction) - invTimeHorizonObst * radius_ >= -RVO_EPSILON && det(invTimeHorizonObst * relativePosition2 - orcaLines_[j].point, orcaLines_[j].direction) - invTimeHorizonObst * radius_ >= -RVO_EPSILON) {
alreadyCovered = true;
break;
}
}
if (alreadyCovered) {
continue;
}
/* Not yet covered. Check for collisions. */
// 没处理过,计算距离的平方
const float distSq1 = absSq(relativePosition1);
const float distSq2 = absSq(relativePosition2);
const float radiusSq = sqr(radius_);
// 两个障碍物之间的方向向量
const Vector2 obstacleVector = obstacle2->point_ - obstacle1->point_;
const float s = (-relativePosition1 * obstacleVector) / absSq(obstacleVector);
const float distSqLine = absSq(-relativePosition1 - s * obstacleVector);
Line line;
// 从代码里看这里障碍物只能处理凸多边形,非凸会有问题
// 与左侧碰撞
if (s < 0.0f && distSq1 <= radiusSq) {
/* Collision with left vertex. Ignore if non-convex. */
if (obstacle1->isConvex_) {
// 线是0 方向与碰撞1相反
line.point = Vector2(0.0f, 0.0f);
line.direction = normalize(Vector2(-relativePosition1.y(), relativePosition1.x()));
orcaLines_.push_back(line);
}
continue;
}
else if (s > 1.0f && distSq2 <= radiusSq) {
// 与右侧碰撞
/* Collision with right vertex. Ignore if non-convex
* or if it will be taken care of by neighoring obstace */
// 方向与碰撞2相反
if (obstacle2->isConvex_ && det(relativePosition2, obstacle2->unitDir_) >= 0.0f) {
line.point = Vector2(0.0f, 0.0f);
line.direction = normalize(Vector2(-relativePosition2.y(), relativePosition2.x()));
orcaLines_.push_back(line);
}
continue;
}
else if (s >= 0.0f && s < 1.0f && distSqLine <= radiusSq) {
/* Collision with obstacle segment. */
// 已经碰上了,方向直接与1相反即可
line.point = Vector2(0.0f, 0.0f);
line.direction = -obstacle1->unitDir_;
orcaLines_.push_back(line);
continue;
}
/*
* No collision.
* Compute legs. When obliquely viewed, both legs can come from a single
* vertex. Legs extend cut-off line when nonconvex vertex.
*/
Vector2 leftLegDirection, rightLegDirection;
// 没看懂,大概就是在区分到底是障碍物1起作用还是障碍物2起作用
if (s < 0.0f && distSqLine <= radiusSq) {
/*
* Obstacle viewed obliquely so that left vertex
* defines velocity obstacle.
*/
if (!obstacle1->isConvex_) {
/* Ignore obstacle. */
continue;
}
obstacle2 = obstacle1;
const float leg1 = std::sqrt(distSq1 - radiusSq);
leftLegDirection = Vector2(relativePosition1.x() * leg1 - relativePosition1.y() * radius_, relativePosition1.x() * radius_ + relativePosition1.y() * leg1) / distSq1;
rightLegDirection = Vector2(relativePosition1.x() * leg1 + relativePosition1.y() * radius_, -relativePosition1.x() * radius_ + relativePosition1.y() * leg1) / distSq1;
}
else if (s > 1.0f && distSqLine <= radiusSq) {
/*
* Obstacle viewed obliquely so that
* right vertex defines velocity obstacle.
*/
if (!obstacle2->isConvex_) {
/* Ignore obstacle. */
continue;
}
obstacle1 = obstacle2;
const float leg2 = std::sqrt(distSq2 - radiusSq);
leftLegDirection = Vector2(relativePosition2.x() * leg2 - relativePosition2.y() * radius_, relativePosition2.x() * radius_ + relativePosition2.y() * leg2) / distSq2;
rightLegDirection = Vector2(relativePosition2.x() * leg2 + relativePosition2.y() * radius_, -relativePosition2.x() * radius_ + relativePosition2.y() * leg2) / distSq2;
}
else {
/* Usual situation. */
if (obstacle1->isConvex_) {
const float leg1 = std::sqrt(distSq1 - radiusSq);
leftLegDirection = Vector2(relativePosition1.x() * leg1 - relativePosition1.y() * radius_, relativePosition1.x() * radius_ + relativePosition1.y() * leg1) / distSq1;
}
else {
/* Left vertex non-convex; left leg extends cut-off line. */
leftLegDirection = -obstacle1->unitDir_;
}
if (obstacle2->isConvex_) {
const float leg2 = std::sqrt(distSq2 - radiusSq);
rightLegDirection = Vector2(relativePosition2.x() * leg2 + relativePosition2.y() * radius_, -relativePosition2.x() * radius_ + relativePosition2.y() * leg2) / distSq2;
}
else {
/* Right vertex non-convex; right leg extends cut-off line. */
rightLegDirection = obstacle1->unitDir_;
}
}
/*
* Legs can never point into neighboring edge when convex vertex,
* take cutoff-line of neighboring edge instead. If velocity projected on
* "foreign" leg, no constraint is added.
*/
// 寻找上一个障碍物
const Obstacle *const leftNeighbor = obstacle1->prevObstacle_;
bool isLeftLegForeign = false;
bool isRightLegForeign = false;
if (obstacle1->isConvex_ && det(leftLegDirection, -leftNeighbor->unitDir_) >= 0.0f) {
/* Left leg points into obstacle. */
leftLegDirection = -leftNeighbor->unitDir_;
isLeftLegForeign = true;
}
if (obstacle2->isConvex_ && det(rightLegDirection, obstacle2->unitDir_) <= 0.0f) {
/* Right leg points into obstacle. */
rightLegDirection = obstacle2->unitDir_;
isRightLegForeign = true;
}
/* Compute cut-off centers. */
const Vector2 leftCutoff = invTimeHorizonObst * (obstacle1->point_ - position_);
const Vector2 rightCutoff = invTimeHorizonObst * (obstacle2->point_ - position_);
const Vector2 cutoffVec = rightCutoff - leftCutoff;
/* Project current velocity on velocity obstacle. */
/* Check if current velocity is projected on cutoff circles. */
const float t = (obstacle1 == obstacle2 ? 0.5f : ((velocity_ - leftCutoff) * cutoffVec) / absSq(cutoffVec));
const float tLeft = ((velocity_ - leftCutoff) * leftLegDirection);
const float tRight = ((velocity_ - rightCutoff) * rightLegDirection);
if ((t < 0.0f && tLeft < 0.0f) || (obstacle1 == obstacle2 && tLeft < 0.0f && tRight < 0.0f)) {
/* Project on left cut-off circle. */
const Vector2 unitW = normalize(velocity_ - leftCutoff);
line.direction = Vector2(unitW.y(), -unitW.x());
line.point = leftCutoff + radius_ * invTimeHorizonObst * unitW;
orcaLines_.push_back(line);
continue;
}
else if (t > 1.0f && tRight < 0.0f) {
/* Project on right cut-off circle. */
const Vector2 unitW = normalize(velocity_ - rightCutoff);
line.direction = Vector2(unitW.y(), -unitW.x());
line.point = rightCutoff + radius_ * invTimeHorizonObst * unitW;
orcaLines_.push_back(line);
continue;
}
// 不知道在干嘛,感觉前面是在计算障碍物是在左侧还是右侧,这里就根据这个来确定project
/*
* Project on left leg, right leg, or cut-off line, whichever is closest
* to velocity.
*/
const float distSqCutoff = ((t < 0.0f || t > 1.0f || obstacle1 == obstacle2) ? std::numeric_limits<float>::infinity() : absSq(velocity_ - (leftCutoff + t * cutoffVec)));
const float distSqLeft = ((tLeft < 0.0f) ? std::numeric_limits<float>::infinity() : absSq(velocity_ - (leftCutoff + tLeft * leftLegDirection)));
const float distSqRight = ((tRight < 0.0f) ? std::numeric_limits<float>::infinity() : absSq(velocity_ - (rightCutoff + tRight * rightLegDirection)));
if (distSqCutoff <= distSqLeft && distSqCutoff <= distSqRight) {
/* Project on cut-off line. */
line.direction = -obstacle1->unitDir_;
line.point = leftCutoff + radius_ * invTimeHorizonObst * Vector2(-line.direction.y(), line.direction.x());
orcaLines_.push_back(line);
continue;
}
else if (distSqLeft <= distSqRight) {
/* Project on left leg. */
if (isLeftLegForeign) {
continue;
}
line.direction = leftLegDirection;
line.point = leftCutoff + radius_ * invTimeHorizonObst * Vector2(-line.direction.y(), line.direction.x());
orcaLines_.push_back(line);
continue;
}
else {
/* Project on right leg. */
if (isRightLegForeign) {
continue;
}
line.direction = -rightLegDirection;
line.point = rightCutoff + radius_ * invTimeHorizonObst * Vector2(-line.direction.y(), line.direction.x());
orcaLines_.push_back(line);
continue;
}
}
其他agent
这个里面有些地方我也没看明白,希望有人能解答就好了。
// timehorizon 是个不明确的含义,具体是什么意思要从代码里探究
// 我的理解是它是指视野,相当于是观测预判多少范围的含义
// 将timehorizon倒数
const float invTimeHorizon = 1.0f / timeHorizon_;
/* Create agent ORCA lines. */
for (size_t i = 0; i < agentNeighbors_.size(); ++i) {
// 拿到其相邻的agent
const Agent *const other = agentNeighbors_[i].second;
// 相对位置
const Vector2 relativePosition = other->position_ - position_;
// 相对速度
const Vector2 relativeVelocity = velocity_ - other->velocity_;
// 当前距离的平方
const float distSq = absSq(relativePosition);
// 碰撞最小距离
const float combinedRadius = radius_ + other->radius_;
// 碰撞最小距离的平方
const float combinedRadiusSq = sqr(combinedRadius);
Line line;
Vector2 u;
if (distSq > combinedRadiusSq) {
// 如果二者还未碰撞
/* No collision. */
// 相对速度 - 相对位置/视野时间
// 或者说 相对速度 - 相对位置/最大容忍的碰撞时间 = 就可以直到相对于预期碰撞来说,这个速度是大了还是小了
/// 感觉这个值应该就是表示当前速度和预期碰撞的速度的差=我们这里简称为碰撞速度差
const Vector2 w = relativeVelocity - invTimeHorizon * relativePosition;
/* Vector from cutoff center to relative velocity. */
// 速度值的平方
const float wLengthSq = absSq(w);
// 内积1 = 碰撞速度差*相对位置 其实就可以用来计算角度差
const float dotProduct1 = w * relativePosition;
// 内积1小于0 并且 内积的值 > 最小距离*碰撞速度差
// 其实就是夹角的大小 小于0 表示是钝角 其实也就是不容易碰撞
if (dotProduct1 < 0.0f && sqr(dotProduct1) > combinedRadiusSq * wLengthSq) {
/* Project on cut-off circle. */
const float wLength = std::sqrt(wLengthSq);
// 归一化
const Vector2 unitW = w / wLength;
// 方向,不知道为什么 这里x取了反方向
line.direction = Vector2(unitW.y(), -unitW.x());
// 预期碰撞速度 - 碰撞速度差)* 方向向量 = 可选速度? 或者说这个是不可选速度
// 应该选择的速度都需要避开这个u,才能让新速度不会往碰撞的方向走
u = (combinedRadius * invTimeHorizon - wLength) * unitW;
}
else {
// 这里对应的就是锐角,可能碰撞
/* Project on legs. */
// 得到距离差
const float leg = std::sqrt(distSq - combinedRadiusSq);
// 这里就看不懂了,求了这两个东西的一个行列式
// 感觉就是区分是在RVO的左侧还是右侧?
if (det(relativePosition, w) > 0.0f) {
/* Project on left leg. */
line.direction = Vector2(relativePosition.x() * leg - relativePosition.y() * combinedRadius, relativePosition.x() * combinedRadius + relativePosition.y() * leg) / distSq;
}
else {
// 在右侧
/* Project on right leg. */
line.direction = -Vector2(relativePosition.x() * leg + relativePosition.y() * combinedRadius, -relativePosition.x() * combinedRadius + relativePosition.y() * leg) / distSq;
}
// 内积2 = 相对速度 投影 到这条线上的长度
const float dotProduct2 = relativeVelocity * line.direction;
// 这个长度*线的方向 - 相对速度 = 不可选速度 类似上面的u
u = dotProduct2 * line.direction - relativeVelocity;
}
}
else {
// 二者已经碰撞了 这里比较奇怪,结合之前别人的说明,就是碰撞了,也会计算计算?
// 直接就无视了碰撞
/* Collision. Project on cut-off circle of time timeStep. */
// 这个直接变成了 1 / 模拟步长了 ,相当于是10
const float invTimeStep = 1.0f / sim_->timeStep_;
// 得到速度差?
/* Vector from cutoff center to relative velocity. */
const Vector2 w = relativeVelocity - invTimeStep * relativePosition;
const float wLength = abs(w);
const Vector2 unitW = w / wLength;
// 反正又得到了一个速度 x 然后 u也得到了
line.direction = Vector2(unitW.y(), -unitW.x());
u = (combinedRadius * invTimeStep - wLength) * unitW;
}
// 然后这条线的起始点 = 老速度+0.5*新速度
line.point = velocity_ + 0.5f * u;
// 加入求解队列
orcaLines_.push_back(line);
}
size_t lineFail = linearProgram2(orcaLines_, maxSpeed_, prefVelocity_, false, newVelocity_);
// 求解失败了,选择用规划3
if (lineFail < orcaLines_.size()) {
linearProgram3(orcaLines_, numObstLines, lineFail, maxSpeed_, newVelocity_);
}
接下来就是3个线性规划,默认是先2,再1,如果都失败了就用3,3调整以后继续调2,直到得到一个解
线性规划1
线性规划1比较难看懂
bool linearProgram1(const std::vector<Line> &lines, size_t lineNo, float radius, const Vector2 &optVelocity, bool directionOpt, Vector2 &result)
{// if (!linearProgram1(lines, i, radius, optVelocity, directionOpt, result)) {
// 这个点乘很奇怪
const float dotProduct = lines[lineNo].point * lines[lineNo].direction;
// 判别式
const float discriminant = sqr(dotProduct) + sqr(radius) - absSq(lines[lineNo].point);
if (discriminant < 0.0f) {
// 直接求解无效
/* Max speed circle fully invalidates line lineNo. */
return false;
}
const float sqrtDiscriminant = std::sqrt(discriminant);
float tLeft = -dotProduct - sqrtDiscriminant;
float tRight = -dotProduct + sqrtDiscriminant;
for (size_t i = 0; i < lineNo; ++i) {
// 分母 分子
const float denominator = det(lines[lineNo].direction, lines[i].direction);
const float numerator = det(lines[i].direction, lines[lineNo].point - lines[i].point);
// 判0
if (std::fabs(denominator) <= RVO_EPSILON) {
// 认定二者平行
/* Lines lineNo and i are (almost) parallel. */
if (numerator < 0.0f) {
return false;
}
else {
continue;
}
}
const float t = numerator / denominator;
if (denominator >= 0.0f) {
/* Line i bounds line lineNo on the right. */
tRight = std::min(tRight, t);
}
else {
/* Line i bounds line lineNo on the left. */
tLeft = std::max(tLeft, t);
}
if (tLeft > tRight) {
return false;
}
}
if (directionOpt) {
/* Optimize direction. */
if (optVelocity * lines[lineNo].direction > 0.0f) {
/* Take right extreme. */
result = lines[lineNo].point + tRight * lines[lineNo].direction;
}
else {
/* Take left extreme. */
result = lines[lineNo].point + tLeft * lines[lineNo].direction;
}
}
else {
/* Optimize closest point. */
const float t = lines[lineNo].direction * (optVelocity - lines[lineNo].point);
if (t < tLeft) {
result = lines[lineNo].point + tLeft * lines[lineNo].direction;
}
else if (t > tRight) {
result = lines[lineNo].point + tRight * lines[lineNo].direction;
}
else {
result = lines[lineNo].point + t * lines[lineNo].direction;
}
}
return true;
}
线性规划2
size_t linearProgram2(const std::vector<Line> &lines, float radius, const Vector2 &optVelocity, bool directionOpt, Vector2 &result)
{ //linearProgram2(orcaLines_, maxSpeed_, prefVelocity_, false, newVelocity_);
// 如果优化方向的话,其实应该是没有障碍的情况,直接输出
if (directionOpt) {
/*
* Optimize direction. Note that the optimization velocity is of unit
* length in this case.
*/
// 速度结果就是目标方向*最大速度
result = optVelocity * radius;
}
// 如果目标速度比最大速度要大
else if (absSq(optVelocity) > sqr(radius)) {
// 直接归一化
// 但是实际上目标速度在外部被归一化过了,相当于是只有一个方向的含义,并没有实际上的物理意义
// 而代码里却在这里比较大小,相当于是有实际的物理意义
// 所以实际用的时候目标速度应该想办法换算成具有物理意义的速度,而不是单独的一个方向含义
// 不过只取方向含义,有简化复杂度的想法吧,相当于不用考虑每个循环后应该取一个什么样的速度
// 相当于做了一个解耦处理,把速度和方向控制给到了更上层去处理吧
/* Optimize closest point and outside circle. */
result = normalize(optVelocity) * radius;
}
else {
// 新速度就等于目标速度
/* Optimize closest point and inside circle. */
result = optVelocity;
}
for (size_t i = 0; i < lines.size(); ++i) {
if (det(lines[i].direction, lines[i].point - result) > 0.0f) {
// 当前速度不满足约束,所以要重新计算这个速度
/* Result does not satisfy constraint i. Compute new optimal result. */
const Vector2 tempResult = result;
// 用当前的约束和参数,用线性规划1来处理
if (!linearProgram1(lines, i, radius, optVelocity, directionOpt, result)) {
// 如果线性规划1也无法处理,那就返回交给线性规划3去处理
result = tempResult;
return i;
}
}
}
// 返回满足约束的数量
return lines.size();
}
线性规划3
这个3就更看不懂了
void linearProgram3(const std::vector<Line> &lines, size_t numObstLines, size_t beginLine, float radius, Vector2 &result)
{// linearProgram3(orcaLines_, numObstLines, lineFail, maxSpeed_, newVelocity_);
float distance = 0.0f;
for (size_t i = beginLine; i < lines.size(); ++i) {
if (det(lines[i].direction, lines[i].point - result) > distance) {
/* Result does not satisfy constraint of line i. */
std::vector<Line> projLines(lines.begin(), lines.begin() + static_cast<ptrdiff_t>(numObstLines));
for (size_t j = numObstLines; j < i; ++j) {
Line line;
float determinant = det(lines[i].direction, lines[j].direction);
if (std::fabs(determinant) <= RVO_EPSILON) {
/* Line i and line j are parallel. */
if (lines[i].direction * lines[j].direction > 0.0f) {
/* Line i and line j point in the same direction. */
continue;
}
else {
/* Line i and line j point in opposite direction. */
line.point = 0.5f * (lines[i].point + lines[j].point);
}
}
else {
line.point = lines[i].point + (det(lines[j].direction, lines[i].point - lines[j].point) / determinant) * lines[i].direction;
}
line.direction = normalize(lines[j].direction - lines[i].direction);
projLines.push_back(line);
}
const Vector2 tempResult = result;
if (linearProgram2(projLines, radius, Vector2(-lines[i].direction.y(), lines[i].direction.x()), true, result) < projLines.size()) {
/* This should in principle not happen. The result is by definition
* already in the feasible region of this linear program. If it fails,
* it is due to small floating point error, and the current result is
* kept.
*/
result = tempResult;
}
distance = det(lines[i].direction, lines[i].point - result);
}
}
}
RVO3D
同理RVO3D,代码结构非常像,但是2d求解的时候是用线,3d的时候就上升到面了,相同问题解算的部分都看不懂。
Summary
大概就这么多,我看得有点云里雾里得。
能找到的参考都在下面了,有2个blog写的还是比较简单易懂的
之前在没看懂的情况下就直接使用了RVO,想到我当时怎么操作都得不到结果,直到我看明白论文才知道。
我当时想给RVO3D的速度的最大值变成三维的,即maxSpeed是一个向量而不是现在的标量,同时再加上一个acc约束,然后我就直接改了最后的update函数,将求解后的速度再次进行约束,然后发现怎么跑都不行。
最后增加约束会破坏原有的RVO无碰撞的基础理论,要增加就必须在他求解线性规划的时候计算,这就比较复杂了,最后放弃了。
Quote
https://gamma.cs.unc.edu/RVO/
https://gamma.cs.unc.edu/ORCA/
https://gamma.cs.unc.edu/RVO2/
Paper:Reciprocal Velocity Obstacles for Real-Time Multi-Agent Navigation
http://www.meltycriss.com/2017/01/13/paper-rvo/
https://zsummer.github.io/2019/06/08/2019-06-08-rvo/
http://www.meltycriss.com/2017/01/14/paper-orca/