Foreword
在看Blender-Molecular-Script源码的时候突然看到了几个不认识的,就记录一下
https://github.com/scorpion81/Blender-Molecular-Script
KD-Tree
k-dimensional,是一种用于分割k维数据空间的数据结构。
先说问题,平常的一维查找,要么挨个比一下,要么二分查找,再复杂一点就是用BST。但是这只是针对一维的数据,如果上升到二维的时候,就无法用单个数值建立对应的二分查找树了。那么这个时候KD-Tree就可以解决这个问题,从理论高度上来说KD-Tree就是BST的抽象类,它本身可以根据不同的适用情况来选择具体建立二分查找树的策略,进而提升查找效率。
- BST,二分查找树
BST的时候是按照大小进行建树的,KDT就不是了,他是按照下面的逻辑进行循环建立的。
-
建立根节点;
-
选取方差最大的特征作为分割特征;
-
选择该特征的中位数作为分割点;
-
将数据集中该特征小于中位数的传递给根节点的左儿子,大于中位数的传递给根节点的右儿子;
-
递归执行步骤2-4,直到所有数据都被建立到KD Tree的节点上为止。
KD Tree的算法复杂度介于O(Log2(N))和O(N)之间,
从几何意义上来讲,如果数据是落在一条线上的,那么显然,通过一个点就能将线二分。
如果数据是落在二维平面上的,那么显然要通过一条线来二分,划分的依据自然就是点到直线的距离了

同理,要想三维度空间中划分,数据显然是要靠一个面,然后点到面的距离。

因为本身是为了搜索服务的,所以建树的策略是必须两端尽可能的平衡,而这个树的根节点就很重要了,相当于他是重心位置,所以一般多选取中点作为根节点。
KNN
- k-nearest neighbors,k近邻算法
简单说就是对一待分类数据进行分类算法,结合上面的KDT,如果来了一个数据,并且可以确定他的位置,那么他属于什么就可以根据他附近的几个已知类型的数据来确定。
而实际中KNN中分类依据来源于以下2点:
- 距离函数,确定未分类数据的位置
- 分类函数,判定未分类数据的归属,其实也就是K-NN中的K如何决定
八叉树
简单说就是将一个立方体分割成8个小立方体,最终达到的效果最好是每一个小立方体中都只包含有一个搜索对象。通过这样的方式来加速空间搜索效率。
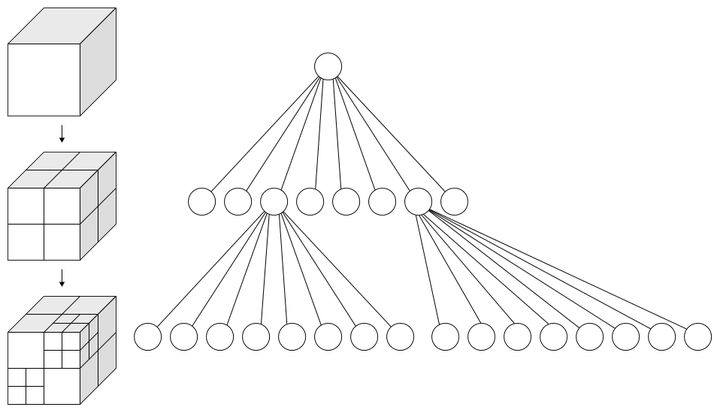
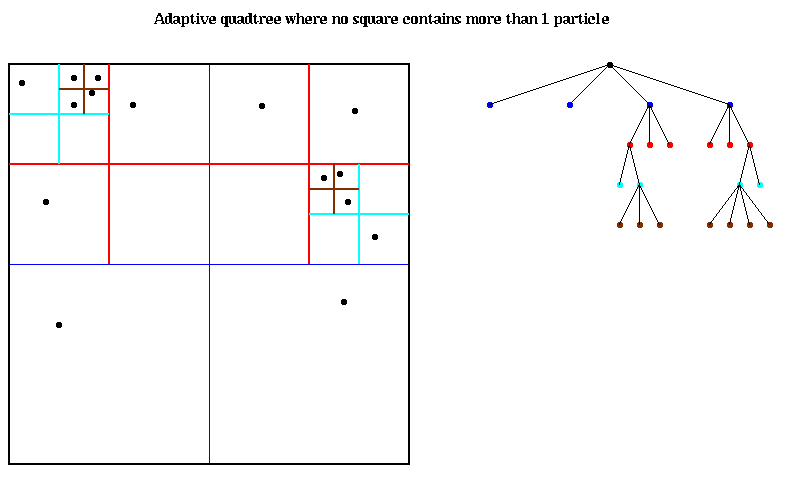
平常在三维空间或者游戏内经常使用,用来判定是否碰撞之类的
Summary
以上三者都是关于空间划分和查找相关的算法,粒子计算中经常需要用到,粒子数量非常大,如果直接遍历效率非常低,所以做粒子自碰撞之类的检测就必须要提高搜索效率。
Quote
https://github.com/scorpion81/Blender-Molecular-Script
https://www.bilibili.com/video/av78028057/
https://zhuanlan.zhihu.com/p/45346117
https://blog.csdn.net/silangquan/article/details/41483689
https://zhuanlan.zhihu.com/p/25994179