61.Count Primes
Description:
Count the number of prime numbers less than a non-negative number, n.
Credits:
Special thanks to @mithmatt for adding this problem and creating all test cases.
Hint:
1.Let’s start with a isPrime function. To determine if a number is prime, we need to check if it is not divisible by any number less than n. The runtime complexity of isPrime function would be O(n) and hence counting the total prime numbers up to n would be O(n2). Could we do better?
2.As we know the number must not be divisible by any number > n / 2, we can immediately cut the total iterations half by dividing only up to n / 2. Could we still do better?
3.Let’s write down all of 12’s factors:
2 × 6 = 12
3 × 4 = 12
4 × 3 = 12
6 × 2 = 12
As you can see, calculations of 4 × 3 and 6 × 2 are not necessary. Therefore, we only need to consider factors up to √n because, if n is divisible by some number p, then n = p × q and since p ≤ q, we could derive that p ≤ √n.
Our total runtime has now improved to O(n1.5), which is slightly better. Is there a faster approach?
public int countPrimes(int n) {
int count = 0;
for (int i = 1; i < n; i++) {
if (isPrime(i)) count++;
}
return count;
}
private boolean isPrime(int num) {
if (num <= 1) return false;
// Loop's ending condition is i * i <= num instead of i <= sqrt(num)
// to avoid repeatedly calling an expensive function sqrt().
for (int i = 2; i * i <= num; i++) {
if (num % i == 0) return false;
}
return true;
}
4.The Sieve of Eratosthenes is one of the most efficient ways to find all prime numbers up to n. But don’t let that name scare you, I promise that the concept is surprisingly simple.
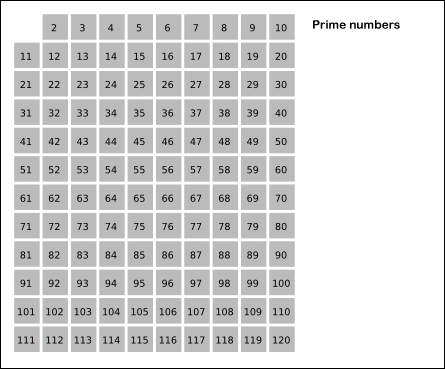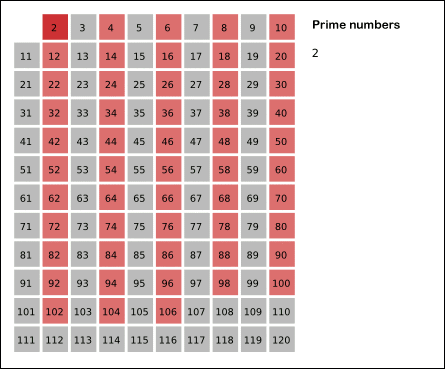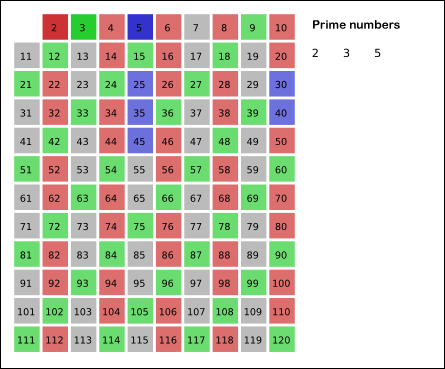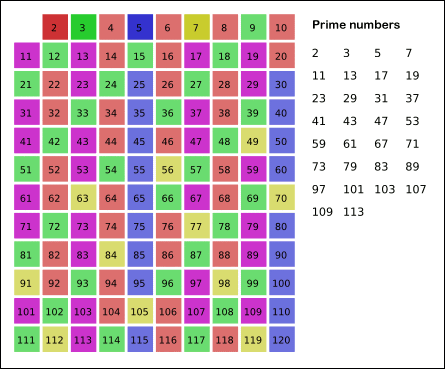
Sieve of Eratosthenes: algorithm steps for primes below 121. “Sieve of Eratosthenes Animation” by SKopp is licensed under CC BY 2.0.
We start off with a table of n numbers. Let’s look at the first number, 2. We know all multiples of 2 must not be primes, so we mark them off as non-primes. Then we look at the next number, 3. Similarly, all multiples of 3 such as 3 × 2 = 6, 3 × 3 = 9, … must not be primes, so we mark them off as well. Now we look at the next number, 4, which was already marked off. What does this tell you? Should you mark off all multiples of 4 as well?
5.4 is not a prime because it is divisible by 2, which means all multiples of 4 must also be divisible by 2 and were already marked off. So we can skip 4 immediately and go to the next number, 5. Now, all multiples of 5 such as 5 × 2 = 10, 5 × 3 = 15, 5 × 4 = 20, 5 × 5 = 25, … can be marked off. There is a slight optimization here, we do not need to start from 5 × 2 = 10. Where should we start marking off?
6.In fact, we can mark off multiples of 5 starting at 5 × 5 = 25, because 5 × 2 = 10 was already marked off by multiple of 2, similarly 5 × 3 = 15 was already marked off by multiple of 3. Therefore, if the current number is p, we can always mark off multiples of p starting at p2, then in increments of p: p2 + p, p2 + 2p, … Now what should be the terminating loop condition?
7.It is easy to say that the terminating loop condition is p < n, which is certainly correct but not efficient. Do you still remember Hint #3?
8.Yes, the terminating loop condition can be p < √n, as all non-primes ≥ √n must have already been marked off. When the loop terminates, all the numbers in the table that are non-marked are prime.
The Sieve of Eratosthenes uses an extra O(n) memory and its runtime complexity is O(n log log n). For the more mathematically inclined readers, you can read more about its algorithm complexity on Wikipedia.
public int countPrimes(int n) {
boolean[] isPrime = new boolean[n];
for (int i = 2; i < n; i++) {
isPrime[i] = true;
}
// Loop's ending condition is i * i < n instead of i < sqrt(n)
// to avoid repeatedly calling an expensive function sqrt().
for (int i = 2; i * i < n; i++) {
if (!isPrime[i]) continue;
for (int j = i * i; j < n; j += i) {
isPrime[j] = false;
}
}
int count = 0;
for (int i = 2; i < n; i++) {
if (isPrime[i]) count++;
}
return count;
}
61.Count Primes-Analysis
神了,这道题竟然有8个线索,只是简单的求素数的个数而已啊?
直接用当前数字/根号(小于等于当前数字) 如果整除了说明不是素数,否则是素数(和线索3相同)。
但是既然不是所有素数,那么就可以用之前的素数来排除后面的成倍数关系的数,而剩下的数则是非素数,并且可以做为下一次排除的依据。(线索四一直到线索八是引导你使用这个筛选法)
61.Count Primes-Solution-C/C++
这是我的写法(直接用当前数字/根号(小于等于当前数字) 如果整除了说明不是素数,否则是素数。),但是一样不出所料Time Limit Exceeded了,所以还得看其他办法
class Solution {
public:
int countPrimes(int n)
{
vector<int> num;
if(n<2)
return 0;
num.push_back(2);
int i=3,j=2;
for(i=3;i<n;i++)
{
for(j=1;j<=sqrt(i);j++)
{
if(i%(j+1)==0)
break;
else
{
if(j+1>=sqrt(i))
{
num.push_back(i);
}
}
}
}
return num.size();
}
};
筛选法,求素数,但是是牺牲空间来换取时间的,用了O(n)的空间才完成的
class Solution {
public:
int countPrimes(int n) {
bool num[n];
int i=0,j=0;
for(i=2;i<n;i++)
{
num[i]=true;
}
for(i=2;i*i<n;i++)
{
if(num[i]==false)
continue;
for(j=i*i;j<n;j=j+i)
{
num[j]=false;
}
}
int count=0;
for(i=2;i<n;i++)
{
if(num[i]==true)
count++;
}
return count;
}
};
61.Count Primes-Solution-Python
python的代码竟然用了1600ms 而上面的C++采用了56ms 而且leetcode的python有bug 时而提示能通过时而提示超时
class Solution(object):
def countPrimes(self, n):
"""
:type n: int
:rtype: int
"""
num=[]
for i in range(n):
num.append(True)
i=2
while i*i<n:
if num[i]==False:
i=i+1
continue
j=i*i
while j<n:
num[j]=False
j=j+i
i=i+1
count=0
for i in range(2,n):
if num[i]==True:
count=count+1
return count
62.Summary Ranges
Given a sorted integer array without duplicates, return the summary of its ranges.
For example, given [0,1,2,4,5,7], return [“0->2”,”4->5”,”7”].
62.Summary Ranges-Analysis
给出一个排序好的数组,且没有重复元素,输出元素的范围。就是元素的连续部分
一样循环,不连续的,就输入到返回区,连续的继续往后
62.Summary Ranges-Solution-C/C++
class Solution
{
public:
vector<string> summaryRanges(vector<int>& nums)
{
if(nums.size()==0)
return (vector<string>)0;
int i=0;
string sline="";
stringstream s;
vector<int>line;
vector<string> ret;
for(i=0;i<nums.size();i++)
{
if(line.size()==0)
{
line.push_back(nums[i]);
}
else if(line.size()==1)
{
if((nums[i]-line[0])==1)
line.push_back(nums[i]);
else
{
//不相同的情况下,把第一个值加入到返回区中
s<<line[0];
s>>sline;
s.clear();
line.clear();
line.push_back(nums[i]);
ret.push_back(sline);
}
}
else
{
if((nums[i]-line[1])==1)
line[1]=nums[i];
else
{
//不相同的情况下,两个值加入到返回区中
s<<line[0]<<"->"<<line[1];
s>>sline;
s.clear();
line.clear();
line.push_back(nums[i]);
ret.push_back(sline);
}
}
}
if(line.size()==1)
s<<line[0];
else
s<<line[0]<<"->"<<line[1];
s>>sline;
s.clear();
ret.push_back(sline);
return ret;
}
};
62.Summary Ranges-Solution-Python
class Solution(object):
def summaryRanges(self, nums):
"""
:type nums: List[int]
:rtype: List[str]
"""
if nums==[]:
return []
ret=[]
line=[]
for i in range(len(nums)):
if len(line)==0:
#当前层没有数据,那么就加入
line.append(nums[i])
elif len(line)==1:
if (nums[i]-line[0])==1:
#当前层有一个数据,判断新数据是否连续
line.append(nums[i])
else:
#数据不连续,加入到返回区
ret.append(line)
#新数据入行
line=[]
line.append(nums[i])
elif len(line)==2:
if (nums[i]-line[1])==1:
#当前层有一个数据,判断新数据是否连续
line[1]=nums[i]
else:
#数据不连续,加入到返回区
ret.append(line)
#新数据入行
line=[]
line.append(nums[i])
ret.append(line)
s=''
sret=[]
for i in range(len(ret)):
if len(ret[i])==1:
s=str(ret[i][0])
sret.append(s)
else:
s=str(ret[i][0])+"->"+str(ret[i][1])
#+"->"+''.join(ret[i][1])
sret.append(s)
return sret
63.First Bad Version
You are a product manager and currently leading a team to develop a new product. Unfortunately, the latest version of your product fails the quality check. Since each version is developed based on the previous version, all the versions after a bad version are also bad.
Suppose you have n versions [1, 2, …, n] and you want to find out the first bad one, which causes all the following ones to be bad.
You are given an API bool isBadVersion(version) which will return whether version is bad. Implement a function to find the first bad version. You should minimize the number of calls to the API.
63.First Bad Version-Analysis
如果有一个版本出现问题,那么之后所有的都会有问题,要求你找到最先出现问题的那个版本。并且调用api的次数越少越好。
毫无疑问二分法就可以了,每次二分,直到找到为止
63.First Bad Version-Solution-C/C++
有一个地方值得注意一下mid=(high+low)/2 但是这么加在大整数的情况下会溢出,所以需要变通一下 mid=low+(high-low)/2 用这样的加法防止溢出的情况
// Forward declaration of isBadVersion API.
bool isBadVersion(int version);
class Solution {
public:
int firstBadVersion(int n)
{
//二分法查找
int low=1,high=n,mid=low+(high-low)/2;
while(low<high)
{
if(isBadVersion(mid)==true)
{
high=mid;
}
else
{
low=mid+1;
}
mid=low+(high-low)/2;//防止越界
}
return mid;
}
};
63.First Bad Version-Solution-Python
# The isBadVersion API is already defined for you.
# @param version, an integer
# @return a bool
# def isBadVersion(version):
class Solution(object):
def firstBadVersion(self, n):
"""
:type n: int
:rtype: int
"""
low=1
high=n
mid=low+(high-low)/2
while low<high:
if isBadVersion(mid)==True:
high=mid
else:
low=mid+1
mid=low+(high-low)/2
return mid
64.Min Stack
Design a stack that supports push, pop, top, and retrieving the minimum element in constant time.
- push(x) – Push element x onto stack.
- pop() – Removes the element on top of the stack.
- top() – Get the top element.
- getMin() – Retrieve the minimum element in the stack.
64.Min Stack-Analysis
构造一个栈,除了基本操作以外,还需要有返回最小值的功能
如果只构造一个栈,用顺序排列,就可以直接返回最小值,但是其他栈的基本操作的返回值会错
所以思路就是构造一个正常栈,构造一个最小栈,需要返回最小值时通过最小栈进行返回,其他内容正常
但是由于时间的限制问题,建立一个完全的最小栈是不可以的,且不说浪费空间,就是时间上也浪费了很多(在把小值插入的过程中)
所以需要一定的优化,可以发现由于是栈的存在,所以并不需要把所有值全都存入最小的栈中。
比如说 push 3 11 3 9 0 3 0 之后 看栈的排列
标准栈 3 11 3 9 0 9 0
最小栈 0 0 3 3 9 9 11 最初的想法
优化栈 3 3 0 0 优化后的栈
当pop getMin 的时候 你会发现,最小值要么在优化栈中,要么在标准栈中
只需要取两者中的最小值就可以得到了.因为删除元素只有pop方法,也就是说只能删除最上面的元素,而minstack只要记录过程中最小的值就可以了
而最小值要么是minstack要么是当前的sdstack中的top值
64.Min Stack-Solution-C/C++
class MinStack
{
public:
stack<int> sd;
stack<int> min;
void push(int x)
{
sd.push(x);
if(min.size()==0||x<=min.top())
min.push(x);
}
void pop()
{
if(min.top()==sd.top())
min.pop();
sd.pop();
}
int top()
{
return sd.top();
}
int getMin()
{
return min.top()<sd.top()?min.top():sd.top();
}
};
64.Min Stack-Solution-Python
理论上说功能上没啥问题,但是超时了,如果只检测getMin的返回时间应该是没有问题的,毕竟是维持了另外一个list 直接返回的
但是还是超时,说明他认为push和pop的操作时间太长了
class MinStack(object):
def __init__(self):
"""
initialize your data structure here.
"""
self.minstack=[]
self.sdstack=[]
def push(self, x):
"""
:type x: int
:rtype: nothing
"""
for i in range(len(self.minstack)):
if x>self.minstack[len(self.minstack)-1-i]:
self.minstack.insert(len(self.minstack)-i,x)
if len(self.minstack)==0:
self.minstack.append(x)
self.sdstack.append(x)
def pop(self):
"""
:rtype: nothing
"""
x=self.sdstack[-1]
del self.sdstack[-1]
for i in range(len(self.minstack)):
if x==self.minstack[i]:
del self.minstack[i]
break;
def top(self):
"""
:rtype: int
"""
return self.sdstack[-1]
def getMin(self):
"""
:rtype: int
"""
if len(self.minstack)!=0:
return self.minstack[0]
else:
return None
优化以后的代码;
class MinStack(object):
def __init__(self):
"""
initialize your data structure here.
"""
self.minstack=[]
self.sdstack=[]
def push(self, x):
"""
:type x: int
:rtype: nothing
"""
if len(self.minstack)==0:
self.minstack.append(x)
elif x<=self.minstack[-1]:
self.minstack.append(x)
self.sdstack.append(x)
def pop(self):
"""
:rtype: nothing
"""
x=self.sdstack[-1]
del self.sdstack[-1]
if len(self.minstack)>0 and x==self.minstack[-1]:
del self.minstack[-1]
def top(self):
"""
:rtype: int
"""
return self.sdstack[-1]
def getMin(self):
"""
:rtype: int
"""
if len(self.minstack)!=0:
return min(self.minstack[-1],self.sdstack[-1])
else:
return 0
Quote
http://blog.csdn.net/xudli/article/details/48286081
http://my.oschina.net/Tsybius2014/blog/505462
http://m.shangxueba.com/jingyan/2926615.html
http://www.cnblogs.com/x1957/p/4086448.html