Foreword
遇到一个匹配问题,搜了很久,就是找不到相关的算法,经过询问,重新描述问题以后,发现原来问题这么简单,而且还有专门描述此类问题的算法。
- 问题: 有若干男孩和女孩,他们之间存在互相喜欢的关系,求一种配对方式使得所有人都能得到喜欢的人(或者是得到最多配对数)
此类问题都有一个共同的数学模型,二分图。图G = (V,E) 是一个无向图,如果一个图可以被分成两部分,并且两部分内部没有任何相连的边,那么这个图就是二分图。
一般是把图中的顶点分成左右两部分,左顶点要和右顶点做一个匹配。
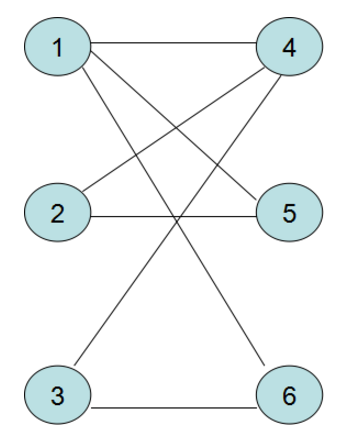
类似于图中1,2,3就是左顶点,4,5,6就是右顶点,顶点之间的边表示可到达,一般遇到匹配问题的时候也会有可到达和不可到达的区别。
二分图有一些特性,一个顶点一定属于左子集或右子集,子集内部顶点不存在边。
二分图判定
一般来说遇到的问题可以明确区分出来是否可以套用二分图。
不过有的时候也需要判断是否可以形成二分图,或者形成的二分图是怎样的。
二分图判定是通过把二分图左侧点全涂成一个颜色,右侧点全涂成一个颜色,如果出现某个点被涂两种颜色,说明其不是二分图。
当然还有一种快速排除的办法,二分图中所有回路其边数必须为偶数,而不能是奇数,出现奇数的情况下就说明有一个点既连接了左侧顶点又连接了右侧顶点。
算法
最简单的算法大概是这样的:
- 选择一个起点,给他设置一个颜色,由它开始进行DFS,每找到一个相连的点设置相反的颜色。
- 把其所有相邻的点都染色后,切换到下一个未染色点。
- 如果出现了下一个点已被染色并且和当前颜色相同,那么说明出现了矛盾(一个点即是黑色又是白色,这在二分图中是不可能出现的),说明当前图不是二分图。
code
const int MAX_V = 1000;
int V, E;
// V 定点数,E边数
vector<int> G[MAX_V];
// 这里使用邻接表,而不是邻接矩阵
// 邻接表的index表示顶点,其内容表示与其相连的顶点
int color[MAX_V];
// 顶点的颜色(只有两种,1或-1,如算法中所有顶点被分成两部分,一个顶点不可能两种颜色)
// 0 表示未染色
bool DFS(int v, int c)
{
color[v] = c;
//将顶点v染成颜色c
for(int i = 0; i < G[v].size(); i++)
{
// 如果邻接点是同色,说明矛盾了
if(color[G[v][i]] == c)
return false;
// 如果邻接点未染色,那么染相反颜色 递归染色
if (color[G[v][i]] == 0 && !dfs(G[v][i], -c))
return false;
}
// 如果都染色了,没有发生矛盾,返回true
return true;
}
void judge()
{
for (int i = 0; i < V; i++)
{
// 如果没染色
if (color[i] == 0)
{
if (!DFS(i, 1))
{
printf("Not Bipartite Graph\n");
return;
}
}
}
printf("Yes,Bipartite Graph\n");
}
二分图最大匹配
要做二分图最大匹配,还需要了解一些概念。
- 匹配:一个边集合,其中任意两条边都没有公共顶点。
- 匹配点:两点形成匹配关系,有边将二者相连的点,且不与其他顶点构成匹配边。
- 匹配边:匹配点之间连成的边。
- 最大匹配:一个二分图中所存在的最大匹配数,称之为最大匹配
- 完美匹配:所有顶点都是匹配点,那么就是完美匹配。
一般来说二分图最大匹配是在二分图的基础上寻找最大的匹配数,相当于是在现有的边的基础上,挑选一些出来作为匹配边,形成一个新图。
比如左图就是一个二分图,二右图中红色的边则是匹配边,其中最大匹配数为4。
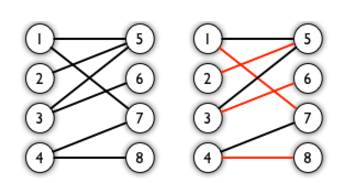
一般来说求解最大匹配数用的是匈牙利算法。
匈牙利算法
匈牙利算法,简单说就是不断的寻找增广路径,从而交换匹配边和非匹配边,进而得到+1匹配数的目的。当整个图被遍历完了以后,那么得到的匹配数就是最大匹配数。
- 增广路:从一个未匹配点出发,先走到非匹配边,再走一条匹配边,走一条非匹配边,再走一条匹配边,一直按照这个非匹配和匹配交替走,如果走到了另一个非匹配点,那么这条路就是增广路.
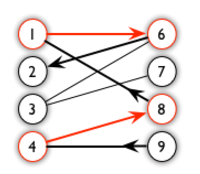
比如图中从9开始,依次是非匹配边,匹配边,非匹配边….一直走到2

可以看到这条路径有一个特性,那就是非匹配边数比匹配边数多一条,而匹配边数,则是上一次找到的,而由于匹配和非匹配边是交错出现的,所以交换二者也不会破坏匹配的性质,从而多了一条匹配边.
那么基于这个原理,使用DFS或者BFS就可以遍历所有边,从而找到最大匹配数.
算法
- 从左边第一个顶点开始,寻找增广路.
- 找到非匹配点,切换匹配和非匹配状态,匹配边数+1
- 没找到,切换下一个顶点.
- 直到把所有顶点搜索完毕.
code
#define maxn 10
// x集合和y集合中顶点的最大个数
int nx, ny;
// x集合和y集合中顶点的个数
int edge_num;
// 已有边数
int edge[maxn][maxn];
// 邻接矩阵,存储当前已有边
int cx[maxn], cy[maxn];
// x,y集合中匹配的顶点
int visited[maxn];
// 记录该顶点是否被访问过
int DFS(int u)
{
int v;
for(v = 0; v<ny; v++)
{
// 存在边 并且没有访问过
if(edge[u][v] && !visited[v])
{
visited[v] = 1;
// 找到非匹配点 或者从该点往下能找到一条增广路
if(cy[v] == -1 || DFS(cy[v]))
{
// 将这两点设置为互相匹配点(匹配和非匹配边交换)
cx[u] = v;
cy[v] = u;
return 1;
}
}
}
return 0;
}
int maxmatch()
{
// 最大匹配数
int res = 0;
memset(cx, -1, sizeof(cx));
memset(cy, -1, sizeof(cy));
//初始值为-1表示两个集合中都没有匹配的顶点
for(int i = 0; i <= nx; i++)
{
if(cx[i] == -1)
{
memset(visited, 0, sizeof(visited));
res += DFS(i);
}
}
return res;
}
Summary
更多详细的二分图相关定义和问题参考下面的引用吧,有很多都写得非常详细了。
Quote
https://www.cnblogs.com/digitalhermit/p/5119908.html
http://blog.csdn.net/thundermrbird/article/details/52231639
http://blog.csdn.net/hackbuteer1/article/details/7398008
http://blog.csdn.net/pi9nc/article/details/11848327
https://www.cnblogs.com/shenben/p/5573788.html
https://www.jianshu.com/p/cb685445e8b1